Large language models (LMs) like ChatGPT provoke new questions about the provenance of written documents. For example, the website StackOverflow has banned users from posting answers using OpenAI’s ChatGPT model to mitigate the spread of misinformation on the platform. However, enforcing a ban on text generated by models is challenging because, by design, these models produce text that appears human-like. A reliable forensic tool for attributing text to a particular language model would empower individuals—such as platform moderators and teachers—to enact and enforce policies on language model usage; it would also better enable model providers to track the (mis)use of their models, e.g., to scrub synthetic text from the training data of future language models.

To achieve provenance, a watermark is a signal embedded within some generated content—in our case, text from a language model (LM)—that encodes the source of the content. In our setting, users access the LM through a trusted LM provider that embeds the watermark in its output. This trust could be underwritten by voluntary commitments, by regulatory compliance, or by law. The user is an untrusted party (e.g., a student who hopes to cheat on a homework assignment) who requests generated text from the LM provider, and may rewrite or paraphrase this text in an effort to remove the watermark. A detector can later check if a piece of text contains the watermark in order to determine whether this text originated from the LM. The detector should be robust to shenanigans by the user: the watermark should remain detectable unless the user has rewritten the text to the extent that it is no longer meaningfully attributable to the LM. The relationship between the LM provider, user, and detector is illustrated by Figure 1.

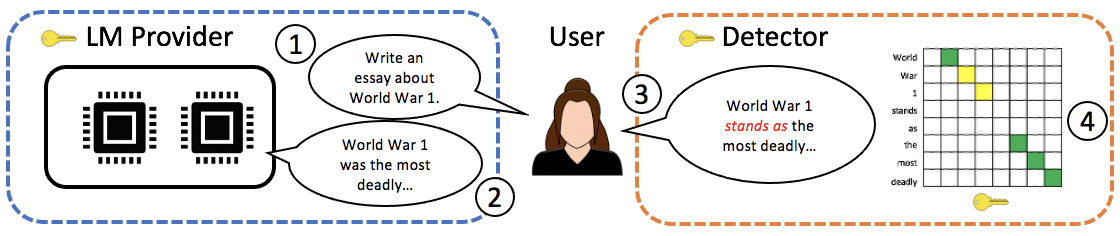
Recent work on watermarking the outputs of an LM proposes to encode a watermark by altering the probability distribution that the LM defines over text. Notably, the watermarks proposed by Kirchenbauer et al. and Aaronson systematically bias outputs of the LM (we give examples in the paper of prompts for which the bias is clearly noticeable qualitatively); a detector can then identify the watermark by checking whether a given text exhibits these biases. In contrast, we want to create watermarks that are distortion-free: the watermark should exactly preserve the original LM’s text distribution, at least up to some maximum number of generated tokens. In particular, our watermarking strategies described below and in the paper are provably distortion-free for the first \(n\) tokens generated by the LM. In practice, we can choose \(n\) to be at least as large as the LM’s context length (and in fact \(n\) can be considerably larger), so that (at the very least) any one interaction with the LM is guaranteed to be distortion-free.

Creating a distortion-free watermark might at first appear impossible: how could a watermark be detectable, if text generated with the watermark is drawn from the same probability distribution as unwatermarked text? The basic idea is to correlate the generated text \(\textbf{text}\) with a random variable \(\xi \sim \nu\), so that the detector can easily distinguish whether some text depends on \(\xi\) (i.e., is watermarked) or is independent (i.e., not watermarked). You can try our watermark detector in the next section, and keep reading below to find out how we generate distortion-free text correlated with the watermark, and how we implement the detector to test for these correlations.

Try the watermark detector

You can run our Javascript implementation of the watermark detector in the text box using the examples we provide below of watermarked text from LLaMA-7B. We configured the detector to test for the watermark key sequence that we used to generate these examples. Edit one of the examples to try to break the watermark!

The detector reports a Monte Carlo estimate of the p-value for observed text (i.e., for the null hypothesis that the text is not watermarked) using a permutation test. For example, thresholding p < 0.01 to determine that text contains the watermark will result in a Type I error rate of 1%. For efficient efficient estimation in the browser, we estimate the p-value using just 100 permutations, leading to a coarse estimate of the p-value; results in the paper report much lower-variance estimates of p-values using 5000 permutations.

Some examples of watermarked text

Here are several examples of watermarked text generated using LLaMA-7B: click to copy text to the detector’s input box. We describe how to generate text with a watermark in the next section (see the \(\texttt{generate-shift}\) algorithm; code for generating watermarked text is implemented here).

He knows that this would cost him the election and his Socialist base and he now clearly prefers a timid path of a slow growth strategy that is reassuring to his base. Some of Hollande's most pro-growth steps have been at their most isolated.

Brewery (now C.V. Richards Brewing Co.) archivist Gilbert Voss. In 2016, a dugout bar opened to accommodate customers. Some of the machines have been brought up to 21st century standards, and some remain as from when the tavern was dedicated.

The struggle of the liberation movement left its mark on the world. "Because of what we achieved the world powers intervened in this country. This remains my memory." Disclaimer: We are not obliged to recommend Mr. Pink or advise our readers.

The SEC-proposed ban on short-selling was a move that would make big investors such as hedge funds significantly more apprehensive. For financial analysts who watch stocks day after day, the catastrophe had an air of the familiar. It was eerily reminiscent of the closings

He opposes increased funding for the California Environmental Protection Agency and big government. He said a couple times that he is a registered cardholder (voter registration card) and votes in every election. He does not even bother attending protests at their LA offices.

Generating and Detecting Watermarked Text

An autoregressive language model defines a probability distribution \(p(\textbf{next}\vert\textbf{prefix})\) over the next token given a prefix. We can iteratively generate text from the model using a decoder to sample the next token from this distribution given a source of randomness, i.e., \(\textbf{next} = \text{Decoder}(p, \xi)\), where \(\xi\) is some random variable. For example, the implementation of \(\text{Decoder}\) could use inverse-transform sampling with \(\xi \sim \text{Uniform}[0,1]\).

function generate(LM, Decoder, prompt, xi) {
  let prefix = prompt.slice();
  for (let i = 0; i < xi.length; i++) {
    probs = LM(prefix);
    nextToken = Decoder(probs, xi[i]);
    prefix.push(nextToken);
  }

  return prefix;
}

Suppose we fix the sequence \(\xi = (\xi_1,\dots,\xi_m)\) to generate text from the LM. A simple idea to determine whether some \(\textbf{text}\) is from the LM is to use \(\xi\) to rerun \(\texttt{generate}\) and compare the output to \(\textbf{text}\). Unfortunately, this idea is a non-starter: we do not know the prompt that the user used to call \(\texttt{generate}\), and checking all prompts to see whether there exists a prompt for which \(\textbf{text} = \texttt{generate}(\text{LM}, \text{Decoder}, \textbf{prompt}, \xi)\) is impractical. Fortunately, the problem is surmountable, and we can build upon the intuitions of this simple idea to construct an effective watermark.

For our watermark, we’ll implement \(\text{Decoder}\) using the Exp-Min trick, as does Aaronson. Let \(\mathcal{V}\) be the vocabulary, and for \(\xi \sim \text{Uniform}[0,1]^{\vert\mathcal{V}\vert}\) and a distribution \(\mu\) over \(\mathcal{V}\), define \(\text{Decode}(\mu, \xi) = \arg \min_{\textbf{token} \in \mathcal{V}} -\frac{1}{p(\textbf{token})} \log \xi.\) Readers may be familiar with the related Gumbel-Max trick, which is popular in the machine learning community for constructing differentiable relaxations of sampling operation. A calculation shows that \(\textbf{token} = \text{Decode}(p,\xi)\) has the correct distribution \(\textbf{token} \sim \mu\). Regardless of the distribution \(\mu\), a large value of \(\xi_\textbf{token}\) will make sampling \(\textbf{token}\) more likely. This observation allows us to construct an ``alignment cost” between a text \(\textbf{text} \in \mathcal{V}^m\) and the sequence \(\xi \in [0,1]^{m\times\vert\mathcal{V}\vert}\) that is agnostic to the prompt:

We can turn this cost into a detector, by searching for a low cost between any possible alignment of \(\xi\) with \(\textbf{text}\). If one of these alignments has a suspiciously low cost, then this is evidence that the text may be watermarked.

function expCost(text, xi, offset) {
  let cost = 0;
  for (let i = 0; i < text.length; i++) {
    cost += Math.log(1-xi[(offset+i)%xi.length][text[i]]);
  }

  return cost;
}

function detect(text, xi) {
  let costs = new Array(text.length);
  for (let j = 0; j < xi.length; j++) {
    costs[j] = expCost(text, xi, j);
  }

  return Math.min(costs);
}

In our formulation thus far, given \(\xi\) the output of \(\texttt{generate}\) is deterministic, which is not ideal in practice: if a user queries the model with the same prompt twice, they will see the same response. One solution for avoiding reusing elements of the watermark key sequence across queries is to make \(\texttt{generate}\) stateful, thus enabling the LM provider to generate a total of \(\lfloor n/m \rfloor\) independent watermarked text samples of \(m\) tokens each from the language model. Instead, to avoid persisting state, we call \(\texttt{generate}\) using a random subsequence of \(\xi\). Concretely, let \(\texttt{shift}(\xi) = \{\xi_{(i+\tau)\%\text{len}(\xi)}\}_{i=1}^m\) where \(\tau \sim \text{Uniform}(\text{len}(\xi))\). We watermark text using the modified generator:

We can thus think of the subsequences of \(\xi\) as comprising a ``codebook” of sorts, in that we generate watermarked text by sampling a length \(m\) codeword from this codebook. Generating watermarked text in this manner does not affect watermark detection, since the detector anyways searches over all subsequences of the watermark key sequence to find the best match for each block of text. Asymptotically, so long as \(n = O(m^c)\) for any constant \(c \in \mathbb{R}\), with high probability (in \(m\)) none of the codewords will be a good match for non-watermarked text relative to the alignment cost between the correct codeword and a watermarked text—even if user replaces some fraction of the tokens in the watermarked text with synonyms. Though in principle different calls to \(\texttt{generate-shift}\) will be correlated (less so for larger \(n\)), in practice we find the effects of these correlations are not noticeable even for smaller \(n\) (e.g., \(n = 256\)).

We can further improve the robustness of the detector using the Levenshtein distance to match codewords with text. In particular, we can replace \(\text{expCost}\) with \(\text{expLevenshteinCost}\) to allow for robustness insertions and deletions of tokens into the text (we assign a cost \(\gamma\) to each insertion/deletion when computing \(\text{expLevenshteinCost}\)). This is the version of the watermark detector implemented for the detection demo above.

function expLevenshteinCost(text, xi, offset, gamma = 0.0) {
  const m = text.length;
  let A = new Array(m+1);
  for (let i = 0; i < m+1; i++) {
    A[i] = new Array(m+1);
    for (let k = 0; k < m+1; k++) {
      if (i === 0) {
        A[i][k] = k * gamma;
      }
      else if (k === 0) {
        A[i][k] = i * gamma;
      }
      else {
        const cost = Math.log(1-xi[(offset+k-1)%xi.length][text[i-1]]);
        A[i][k] = Math.min(A[i-1][k]+gamma, A[i][k-1]+gamma, A[i-1][k-1]+cost);
      }
    }
  }

  return A[m][m];
};

Analysis and Empirical Results

Our main theoretical result on watermark detectability (Lemma 2.8 in the paper) states that if \(\textbf{text}\) was generated from \(\xi\) then, with high probability, the cost of aligning \(\textbf{text}\) with \(\xi\) will be less than the cost of aligning \(\textbf{text}\) with a different (independent) random sequence \(\xi'\). This motivates a practical hypothesis test for watermark detection: simply compare the value of \(\text{detect}(\textbf{text}, \xi)\) to the values of \(\text{detect}(\textbf{text},\xi')\) for resampled random sequences \(\xi'\) that are independent copies of \(\xi\). The detectability of our watermark depends on a quantity of the text itself which we call the watermark potential and define by

For example, a deterministic language model always produces text with zero watermark potential, and the statistical power of any distortion-free watermark will necessarily be zero. We give a lower bound (Lemma 2.2 in the paper) showing the detection accuracy of any watermark (i.e., not just ours) must necessarily depend on the watermark potential of the text. We also show in the paper that instruction-following models, typified by Alpaca 7B, tend to generate text with low watermark potential, which makes these models more difficult to watermark than models for more open-ended text generation.

In particular, for both the OPT-1.3B and LLaMA-7B models, we can reliably detect watermarked text (\(p \leq 0.01\)) from \(35\) tokens even after corrupting between \(40\)-\(50\)% of the tokens via random edits (i.e., substitutions, insertions or deletions); the watermark also remains detectable from \(50\) tokens even after paraphrasing the text by translating to French/Russian and back. For the Alpaca-7B model, we conduct a case study on the feasibility of watermarking responses to typical user instructions. Due to the lower entropy of the responses, detection is more difficult: around \(25\%\) of the responses—whose median length is around \(100\) tokens—are detectable with \(p \leq 0.01\), and the watermark is also less robust to paraphrasing.

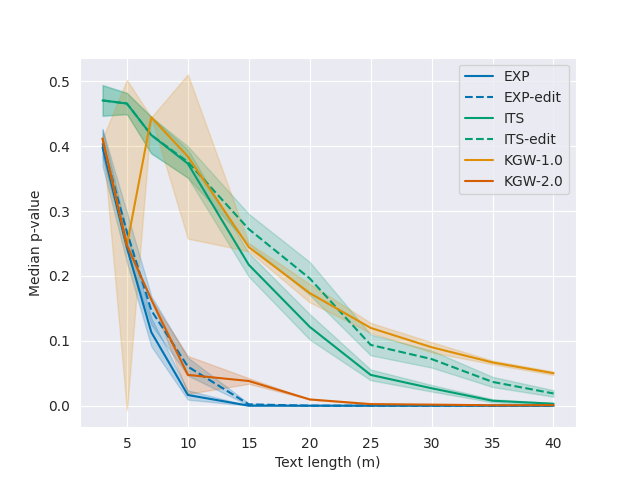
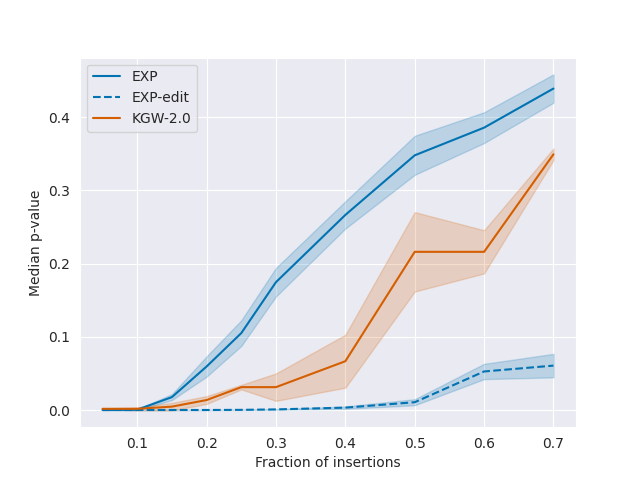
Discussion and Supplementary Material

Recently, several major language model providers (OpenAI, Anthropic, Google, and Meta, among others) have pledged to watermark text generated by their models. Together with proposed regulatory requirements for watermarking in the draft EU AI Act and Chinese policy, it is conceivable that watermarks will become standard for high-profile LM products with large user bases. The distortion-free guarantee of our watermarks shows that imposing this standard is doable at little cost to LM providers.

For more details about our watermarks, and code that implements our watermarking strategies, see the following resources:

• Paper: the paper has additional details, theory, and empirical analysis of the watermarking methodology described in this post.
• Code: a reference implementation for watermarking LM outputs, Python and Javascript implementations of the watermark detector, and scripts for reproducing the experiments featured here and in the paper.

Acknowledgments

The members of this research team belong to the Stanford Center for Research on Foundation Models (CRFM) and the Stanford NLP Group. This work has been supported by an Open Philanthropy Project Award (OpenPhil) and an NSF Frontier Award (NSF Grant no. 1805310).

@article{kuditipudi2023robust,
  title={Robust Distortion-free Watermarks for Language Models},
  author={Kuditipudi, Rohith and Thickstun, John and Hashimoto, Tatsunori and Liang, Percy},
  journal={arXiv preprint arXiv:2307.15593},
  year={2023}
}