HELM Capabilities: Evaluating LMs Capability by Capability
Authors: Jialiang Xu and Yifan Mai and Percy Liang
Introducing HELM Capabilities, a benchmark that evaluates language models across a curated set of key capabilities, providing a comparison of their strengths and weaknesses.
Evaluating language models is a dynamic and critical process as models continue to improve rapidly. Understanding their strengths and weaknesses is essential for external users to determine which models suits their needs. Two years ago, we introduced the Holistic Evaluation of Language Models (HELM) as a framework to assess language models. Using the HELM framework, we have published a series of transparent and reproducible leaderboards, including general-purpose leaderboards for evaluating core capabilities (HELM Classic, HELM Lite), and specialized leaderboards for specific key areas such as safety (AIR-Bench), instruction following (HELM Instruct), and multilinguality (CLEVA, ThaiExam).
Building on the HELM framework, we introduce HELM Capabilities to capture our latest thinking on the evaluation of general capabilities. HELM Capabilities is a new benchmark and leaderboard that consists of a curated set of scenarios for measuring various capabilities of language models. Like all other HELM leaderboards, the HELM Capabilities leaderboard provides full prompt-level transparency, and the results can be fully reproduced using the HELM framework. The latest leaderboard results of HELM Capabilities can be found at https://crfm.stanford.edu/helm/capabilities/latest/.
HELM Capabilities v1.0.0
HELM Capabilities focuses on evaluating language models across scenarios representing core capabilities. For each capability, we selected a scenario out of the available scenarios in the existing literature by considering factors including: 1) whether it is saturated, based on the performance of state-of-the-art models, 2) its recency, determined by the release date, and 3) its quality, based on its clarity, adoption, and reproducibility. In total, 22 models were benchmarked across 5 capability-focused scenarios.
Basic Setup
HELM Capabilities evaluates the following capabilities and scenarios (we show an example from each scenario):
- MMLU-Pro (General Knowledge) extends MMLU to assess models’ knowledge across diverse academic and professional domains, emphasizing multidisciplinary knowledge and depth (Wang et al. 2024).
Question:
The symmetric group $S_n$ has $ \factorial{n}$ elements, hence it is not true that $S_{10}$ has 10 elements. Find the characteristic of the ring 2Z.
Options:[ "0", "30", "3", "10", "12", "50", "2", "100", "20", "5" ]
Answer:0 - GPQA (Reasoning) evaluates models’ ability to reason at a graduate-level complexity across various domains (Rein et al. 2023).
Question:
Two quantum states with energies E1 and E2 have a lifetime of 10^-9 sec and 10^-8 sec, respectively. We want to clearly distinguish these two energy levels. Which one of the following options could be their energy difference so that they be clearly resolved?
Options:[ "10^-4 eV", "10^-11 eV", "10^-8 eV", "10^-9 eV" ]
Answer:10^-4 eV - IFEval (Instruction Following) tests how well models understand and execute user instructions using verifiable instructions (Zhou et al. 2023).
Prompt:
Write a 300+ word summary of the wikipedia page "https://en.wikipedia.org/wiki/Raymond_III,_Count_of_Tripoli". Do not use any commas and highlight at least 3 sections that has titles in markdown format, for example *highlighted section part 1*, *highlighted section part 2*, *highlighted section part 3*.
Judge: Script-based instruction following checker. - WildBench (Dialogue) assesses the models’ ability to engage in dynamic and contextually-aware conversations (Lin et al. 2024).
Conversation Input:
[ { "content": "act as an academic researcher and show a table from credible sources about Hungary's digital economy growth compared to Indonesia's digital economy growth from 2015-2023.", "language": "English", "redacted": false, "role": "user", "toxic": false } ]
Checklist:[ "Does the output include a table comparing Hungary's and Indonesia's digital economy growth from 2015-2023?", ...] - Omni-MATH (Mathematical Reasoning) challenges models with high-level mathematical problem-solving tasks comparable to international mathematical Olympiad competitions (Gao et al. 2024).
Problem:
Let $ n(\ge2) $ be a positive integer. Find the minimum $ m $, so that there exists $x_{ij}(1\le i ,j\le n)$ satisfying: (1)For every $1\le i ,j\le n, x_{ij}=max\{x_{i1},x_{i2},...,x_{ij}\} $ or $ x_{ij}=max\{x_{1j},x_{2j},...,x_{ij}\}.$ (2)For every $1\le i \le n$, there are at most $m$ indices $k$ with $x_{ik}=max\{x_{i1},x_{i2},...,x_{ik}\}.$ (3)For every $1\le j \le n$, there are at most $m$ indices $k$ with $x_{kj}=max\{x_{1j},x_{2j},...,x_{kj}\}.$
Answer:1 + \left\lceil \frac{n}{2} \right\rceil
The key details of each scenario used in HELM Capabilities are as follows:
| Name | Task Type | Metrics | Number of Total Instances | Release Date | Project Page |
|---|---|---|---|---|---|
| MMLU-Pro (Wang et al. 2024) | General Knowledge | Accuracy | 12k downsampled to 1k | Jun’24 | https://github.com/TIGER-AI-Lab/MMLU-Pro |
| GPQA (Rein et al. 2023) | Reasoning | Accuracy | 448 | Nov’23 | https://github.com/idavidrein/gpqa |
| IFEval (Zhou et al. 2023) | Instruction Following | IFEval Strict Accuracy | 541 | Nov’23 | https://github.com/EleutherAI/lm-evaluation-harness/tree/main/lm_eval/tasks/ifeval |
| WildBench (Lin et al. 2024) | Dialogue | WB-Score | 1024 downsampled to 1k | Jun’24 | https://github.com/allenai/WildBench |
| Omni-MATH (Gao et al. 2024) | Mathematical Reasoning | Model-judged Accuracy | 4428 downsampled to 1k | Oct’24 | https://omni-math.github.io/ |
Implementation Details
Overall Architecture. Figure 1 illustrates the architecture used in HELM Capabilities. In the rest of this section, the components are explained following the conceptual order of an instance’s lifecycle.
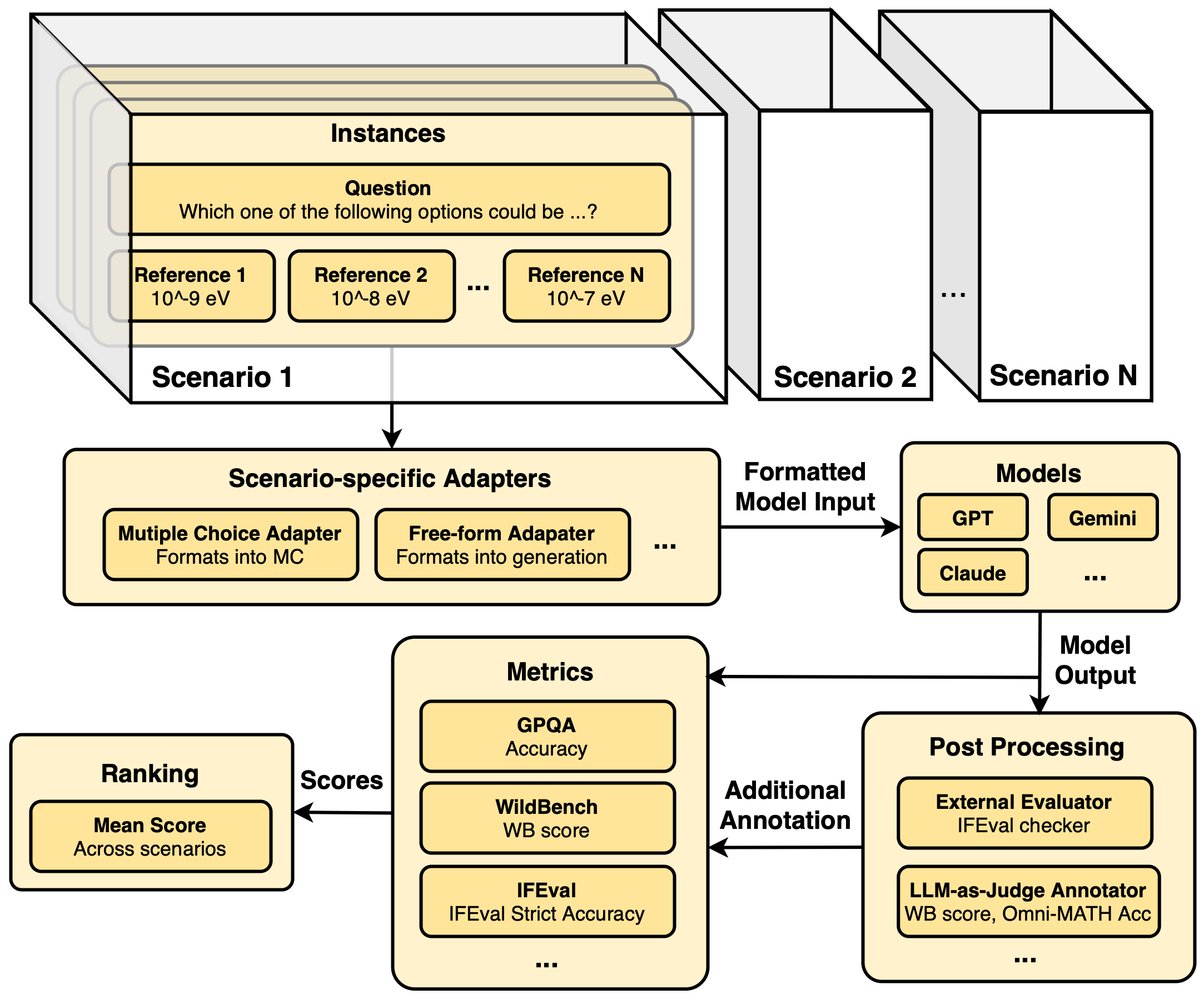
Figure 1: Architecture Diagram for HELM Capabilities.
Scenarios and Instances. Similar to HELM Lite, each scenario in HELM Capabilities consists of a set of instances, each consisting of a textual input and references. However, unlike HELM Lite, only two scenarios in HELM Capabilities (MMLU-Pro and GPQA) are multiple-choice question-answering tasks with reference texts, while the remaining scenarios are free-form generation tasks. All scenarios are downsampled to 1000 instances.
Scenario-specific Adapters. For the multiple-choice question answering tasks (MMLU-Pro and GPQA), we evaluate an instance using zero-shot Chain-of-Thought prompting. For GPQA, IFEval, WildBench, and Omni-MATH, we used the official prompt template from the paper. MMLU-Pro does not have an official prompt template for zero-shot Chain-of-Thought setting, so we used the same prompt template as GPQA. For full transparency, the raw prompts can be viewed on the HELM Capabilities leaderboard.
Models. In HELM Capabilities, we evaluated the following models. We chose these models as they are positioned as the flagship models from mainstream model providers:
- OpenAI: GPT-4o (2024-08-06), GPT-4o mini (2024-07-18)
- Anthropic: Claude 3.5 Haiku (20241022), Claude 3.5 Sonnet (20240620), Claude 3.7 Sonnet (20250219)
- Google: Gemini 1.5 Pro (002), Gemini 1.5 Flash (002), Gemini 2.0 Flash, Gemini 2.0 Flash Lite (02-05 preview)
- Meta: Llama 3.1 Instruct Turbo (8B, 70B, 405B)
- Mistral AI: Mistral Instruct v0.3 (7B), Mixtral Instruct (8x7B, 8x22B)
- Qwen: Qwen2 Instruct Turbo (72B)
- DeepSeek: DeepSeek v3
- Amazon: Amazon Nova (Pro, Lite, Micro)
- Writer: Palmyra-X-004
For models from OpenAI, Anthropic, Google, Amazon, and Writer, we used their official API endpoint. For the Llama, Mistral, and Qwen models, we used the Together AI platform API for model access. For Llama and Qwen models, we used the Turbo variants of the models, which are models that have been quantized using Together AI’s proprietary process.
Postprocessing. The postprocessing step takes the model output as input and generates additional information on it, which can be used in the calculation of metrics (e.g., leveraging LLM-as-a-judge). In HELM Capabilities, we post-process model output via either rules or additional HELM annotators:
- MMLU-Pro and GPQA: a logic utilizing regular expressions to extract the model’s choice among the options from its Chain-of-Thought process.
- IFEval: evaluator logic from the official implementation, which identifies instruction types and verifies instruction fulfillment.
- WildBench: an annotator calls multiple LLMs (GPT-4o (20240513), LLaMA 3.1 405B Instruct Turbo, and Claude 3.5 Sonnet (20241022)) to score a model’s output against a checklist, and takes the average for the final scoring.
- Omni-MATH: an LLM-as-a-judge annotator that compares the model prediction against the gold answer to determine whether they are equivalent. The annotator queries three different LLMs and takes the average of the votes. Note that we deviated from the judging prompt template from the original Omni-MATH paper and used the HELM Safety LLM-as-a-judge prompt. The main reason behind this deviation is that human evaluation on our canary results showed the original prompt encouraged judges’ hallucination on long incorrect model generations and decreased the overall judging accuracy.
Metrics. Metrics for multiple-choice question-answering tasks are straightforward and we chose the overall accuracy for the model choices. The freeform generation tasks are scored either with an external evaluator (IFEval) or an LLM-as-a-judge approach (WildBench, Omni-MATH). Namely, we used the following metrics for scoring:
- MMLU-Pro: Multiple Choice Accuracy.
- GPQA: Multiple Choice Accuracy.
- IFEval: IFEval Strict Accuracy. We chose it over the loose counterpart considering the authors’ recommendation and simplicity.
- WildBench: WB-Score. We chose this over WB-Reward for simplicity and consistency. To reduce variance, we used three LLM-as-a-judge models: GPT-4o (20240513), LLaMA 3.1 405B Instruct Turbo, and Claude 3.5 Sonnet (20241022). The original score is between 1 and 10, we rescale it to the range of 0 and 1 (1 mapped to 0.0 and 10 mapped to 1.0).
- Omni-MATH: LLM-judged Accuracy (LLM judged against gold answers). We chose this metric as it is used to report the results on the main official leaderboard.
Top-level Aggregation. The models are ranked based on the mean score, which aggregates metrics across scenarios with the WB score (1-10) rescaled to 0-1. Note that this is different from our previous approach in HELM Classic and HELM Lite, which is to use the mean win rate as the top-level aggregate score. This change is motivated by the fact that the mean win rate is 1) dependent on the set of models being compared, and 2) sensitive to small variations in scenario scores that invert ranks.
Pipeline Robustness. During the implementation of the leaderboard, we noticed some failure modes for scenarios, and made modifications to address them:
- LLM-as-a-judge requests can fail due to incorrect output formatting from the judge model, which results in a missing judge annotation and often a false negative. In addition, every judge model can have its inherent bias for similar models. We introduced multiple judges for annotations and took the average as the final metric, with the objective of 1) reducing bias in judge results, and 2) providing fall-back alternatives when a subset of all judge requests fail.
- Official implementation might not cover the use case of interest. For example, MMLU-Pro does not have an official prompt for zero-shot Chain-of-thought inference. In this case, we reuse prompts from another scenario. For MMLU-Pro we used GPQA’s prompt.
- The instructions to the model in the prompts can be ambiguous. For example, GPQA has the following instruction in the official prompt:
Format your response as follows: "The correct answer is (insert answer here)". The evaluated language models have interpreted this instruction in various ways and produced a diverse range of output formats that are not captured by the official answer-extraction regular expression, such as “\text{The correct answer is C. }”,**The correct answer is J.**”,The correct answer is G. 4096”,The correct answer is **C**”,The correct answer is **A. Zellweger syndrome**.” We modified the answer-extraction regular expression to account for this. - The instructions to the LLM-as-judge model in the official prompts can be inefficient. The official implementation of Omni-MATH uses a lengthy few-shot prompt. It was observed that in many cases where the model generation is long due to thinking process or low-quality output (e.g., repetitions), this prompt can encourage the judge model to hallucinate on the model answer, leading to erroneous evaluation metrics.
Results and Insights
The top-level aggregate score is as follows:
| Model | Mean score |
|---|---|
| Gemini 2.0 Flash | 0.679 |
| Claude 3.7 Sonnet (20250219) | 0.674 |
| DeepSeek v3 | 0.665 |
| Gemini 1.5 Pro (002) | 0.657 |
| Claude 3.5 Sonnet (20241022) | 0.653 |
| Gemini 2.0 Flash Lite (02-05 preview) | 0.642 |
| GPT-4o (2024-11-20) | 0.634 |
| Llama 3.1 Instruct Turbo (405B) | 0.618 |
| Palmyra-X-004 | 0.609 |
| Gemini 1.5 Flash (002) | 0.609 |
Overall Results. Among the benchmarked models, Gemini 2.0 Flash is at the top of the leaderboard with a mean score of 0.679, primarily due to its high score on Omni-MATH. Claude 3.7 Sonnet (20250219) follows with a strong performance, achieving a mean score of 0.674, demonstrating its edge on MMLU-Pro and GPQA. DeepSeek v3 takes the third spot with a mean score of 0.665, and is also the top open-weight model.
Comparison Across Scenarios. If we look across scenarios, the best-performing model is not consistent and usually not Gemini 2.0 Flash: the best model on MMLU-Pro and GPQA is Claude 3.7 Sonnet (20250219), the best model on IFEval is Palmyra-X-004, and the best model on WildBench is DeepSeek v3. Across all models, Claude 3.7 Sonnet (20250219) and Gemini 1.5 Pro (002) are constantly among the top-5 models. One surprising observation was the comparatively lower accuracy of GPT-4o (2024-08-06) and Claude 3.5 Sonnet (20240620) on the Omni-MATH scenario, which consequently impacted their overall aggregate rankings. This relative underperformance aligns with the results reported in the original paper (Gao et al. 2024). It is observed that GPT-4o (2024-08-06) has a higher tendency to generate responses prone to calculation or logical errors. We refer interested readers to the error analysis section (Appendix A and Figure 8) of the original paper for detailed analysis and comparison with other models.
Comparison Across Model Categories. When examining the performance across model categories, closed models continue to lead in the overall mean score, but open models have also demonstrated competitive performance. Of the top 10 models, two of them are open (DeepSeek v3 on the third place, and Llama 3.1 Instruct Turbo (405B) on the eighth). In particular, DeepSeek v3 achieved best performance on WildBench. Within each model family with known model sizes, larger models outperform their smaller counterparts in all scenarios except Llama on IFEval, where the 405B model underperformed the 70B one.
Comparison with Official Results and External Results. We also compared to those from external sources, including self-reported results, official benchmark results, or third-party leaderboard results, when available. We found that the reported numbers often vary significantly across sources. As an example, see the table below summarzing the numbers on MMLU-Pro from different sources (* denotes self reports): the results can be drastically different and sometimes conflicting (e.g., Qwen2.5 Instruct Turbo (72B)). In the cases where self-reported/official benchmark results and third-party leaderboard results are both available, we found that HELM Capabilities has trends closer to the self-reported/official benchmark results than other third-party leaderboards.
| Model | HELM | OpenLLM | MMLU-Pro Leaderboard |
|---|---|---|---|
| DeepSeek v3 | 0.688 | N/A | 0.7587 |
| Gemini 1.5 Pro (002) | 0.729 | N/A | 0.7025 |
| GPT-4o (2024-08-06) | 0.712 | N/A | 0.7468 |
| Claude 3.5 Sonnet (20240620) | 0.733 | N/A | 0.7612 |
| Llama 3.1 Instruct Turbo (405B) | 0.719 | N/A | 0.733* |
| Llama 3.1 Instruct Turbo (70B) | 0.639 | 0.479 | 0.6284 |
| Qwen2.5 Instruct Turbo (72B) | 0.553 | 0.514 | 0.7159 / 0.581* |
| Gemini 1.5 Flash (002) | 0.641 | N/A | 0.6409 |
| GPT-4o mini (2024-07-18) | 0.61 | N/A | 0.6309 |
| Claude 3.5 Haiku (20241022) | 0.634 | N/A | 0.6212 |
| Qwen2.5 Instruct Turbo (7B) | 0.524 | 0.365 | 0.45* |
| Llama 3.1 Instruct Turbo (8B) | 0.412 | 0.306 | 0.4425 |
| Mixtral Instruct (8x22B) | 0.44 | 0.387 | 0.5633 |
| Mixtral Instruct (8x7B) | 0.336 | 0.299 | 0.4327 |
| Mistral Instruct v0.3 (7B) | 0.279 | 0.230 | N/A |
Typical Success and Failure Cases. We showcase some typical success and failure case examples on each of the scenarios in the Appendix. In general, different models have rather different behavioral patterns, resulting in diverse success and failure modes.
Acknowledgments
We would like to express our gratitude to Siya Goel for assistance in identifying relevant scenarios and contributing to the creation of HELM Capabilities. We would also like to acknowledge the following companies for providing model APIs that were instrumental in this work: Together AI, OpenAI, Google, Anthropic, Amazon, and Writer. Their contributions have been invaluable in enabling the evaluation of a diverse set of language models. HELM Capabilties is funded by the HAI Industrial Affiliates Program.
Appendix: Success and Failure Examples
In this section, we showcase one successful example and one failure example for the best-performing model in each of the scenarios. For the failure example, we also include the reason why they are considered incorrect or low-scoring.
MMLU-Pro
Best performing model: Claude 3.7 Sonnet (20250219)
Success example: Id 1663
Input
What is the relationship between the formal sources of international law?
References
(A) Treaties supersede custom
(B) Treaties and General Principles of Law are of equal importance, but both supersede custom
(C) General Principles of Law supersede both custom and treaties
(D) Judicial decisions and teachings of the most highly qualified publicists are the only sources of international law.
(E) Judicial decisions and teachings of the most highly qualified publicists supersede both custom and treaties
(F) Custom and General Principles of Law are of equal importance, but both supersede treaties
(G) There is a hierarchy, but it varies from case to case
(H) Custom supersedes treaties
(I) Treaties and custom are of equal importance, but General Principles of Law supersede both
(J) There is no hierarchy between the formal sources of international law (correct)
Prediction raw text
To answer this question, I need to analyze the relationship between the formal sources of international law as defined in Article 38 of the Statute of the International Court of Justice.
The formal sources of international law are:
1. International conventions/treaties
2. International custom
3. General principles of law
4. Judicial decisions and teachings of highly qualified publicists (as subsidiary means)
The key point in international law is that there is no formal hierarchy established between treaties, custom, and general principles of law. They are generally considered to coexist without a predetermined order of precedence. Specific rules like lex specialis (specific law prevails over general law) or lex posterior (later law prevails over earlier law) may apply in specific cases, but there is no blanket hierarchy.
Judicial decisions and the teachings of publicists are considered subsidiary means for determining rules of law, not primary sources themselves.
Looking at the options, only answer J correctly reflects this understanding.
The correct answer is J.
Failure example: Id 8603
Reason: arithmetic error (“2K/15 = 2K/30”)
Input
Compute the area of the triangle whose altitudes have lengths 10, 12, and 15.
References
(A) 56\sqrt{15}
(B) 60\sqrt{7}
(C) 240\sqrt{7}/7 (correct)
(D) 48\sqrt{15}
(E) 120\sqrt{15}
(F) 180\sqrt{7}/7
(G) 60\sqrt{7}/7
(H) 48\sqrt{7}
(I) 100\sqrt{7}
(J) 240\sqrt{7}
Prediction raw text
I'll solve this step by step.
For a triangle with area K and side lengths a, b, c, the altitude to side a is h_a = 2K/a. Similarly for the other sides.
Let's denote the altitudes as h_a = 10, h_b = 12, and h_c = 15, and the area as K.
This gives us:
- 10 = 2K/a
- 12 = 2K/b
- 15 = 2K/c
Solving for the sides:
- a = 2K/10 = K/5
- b = 2K/12 = K/6
- c = 2K/15 = 2K/30
Using the formula K = √(s(s-a)(s-b)(s-c)) where s = (a+b+c)/2:
s = (K/5 + K/6 + 2K/30)/2 = (6K/30 + 5K/30 + 2K/30)/2 = 13K/60
Substituting into the area formula and solving the resulting equation:
K = √(s(s-a)(s-b)(s-c))
K = √((13K/60)((13K/60-K/5)(13K/60-K/6)(13K/60-2K/30)))
After algebraic manipulation, this simplifies to K = 60√7.
The correct answer is B. 60\sqrt{7}
GPQA
Best performing model: Claude 3.7 Sonnet (20250219)
Success example: Id 0
Input
A large gene has dozens of exons, of which the central ones code for folded triple helical repeats that connect the cytoskeleton with sarcolemma and extracellular space. Each exon usually codes for one folded triple alpha helix. The most common mutations of the gene are central exon deletions that create out-of-frame peptides and progressive degenerative organ waste. A solution is to deliver a Morpholino that recognizes the 5' end of the out-of-frame exon in pre-mRNA. The molecule prevents binding of the spliceosome and creates exon skipping and in-frame joining. Several missing exons are well tolerated by an organism. Which structure below is not involved in the proposed therapy?
References
(A) polyA tail
(B) lariat
(C) antisense
(D) R-loops (correct)
Prediction raw text
I need to analyze what's involved in the described exon skipping therapy using Morpholinos.
The therapy uses Morpholinos (antisense oligonucleotides) that bind to the 5' end of an out-of-frame exon in pre-mRNA. This prevents spliceosome binding, causing the exon to be skipped, resulting in an in-frame transcript.
Looking at each option:
- Polymerase A tail: This is added to mature mRNA after transcription but isn't directly involved in splicing or the Morpholino mechanism.
- Lariat: This is an intermediate structure formed during splicing when the spliceosome processes pre-mRNA.
- Antisense: The Morpholino itself is an antisense oligonucleotide that binds to the target sequence.
- R-loops: These are RNA-DNA hybrid structures that form during transcription but aren't directly involved in the described therapy.
The correct answer is (D) R-loops.
Failure example: Id 6
Reason: reasoning error (given 2 set of equivalent protons, should reduce signal number by 2, but only reduced by 1. The p‐substituted benzene ring bearing the sulfonate and the azo group is not giving four separate proton signals. Para substitution enforces a plane of symmetry, meaning the four aromatic protons in that ring collapse into two sets of chemically equivalent protons—not three or four.)
Input
aniline is heated with sulfuric acid, forming product 1.
1 is treated with sodium bicarbonate, followed by sodium nitrite and HCl, forming product 2.
2 is allowed to react with 2-napthol, forming final product 3.
how many distinct nonexchaning hydrogen signals are there in the 1H nmr spectrum of 3?
References
(A) 6
(B) 9
(C) 8 (correct)
(D) 7
Prediction raw text
To determine the answer, I need to identify product 3 and analyze its 1H NMR spectrum.
Step 1: Identify product 1
When aniline (C6H5NH2) is heated with sulfuric acid, sulfanilic acid (p-aminobenzenesulfonic acid) is formed. This places the sulfonic acid group (-SO3H) para to the amino group.
Step 2: Identify product 2
Treatment with NaHCO3 neutralizes the sulfonic acid to form a sulfonate salt. Then sodium nitrite and HCl perform a diazotization reaction on the amino group, forming a diazonium salt (p-sulfobenzenediazonium chloride).
Step 3: Identify product 3
The diazonium salt reacts with 2-naphthol in an azo coupling reaction, forming an azo dye. The diazonium group couples at the 1-position of 2-naphthol (para to the OH group).
Step 4: Count non-exchanging hydrogen signals in product 3
The final structure has:
- 4 distinct hydrogens on the benzene ring with the sulfonate group
- 6 distinct hydrogens on the naphthalene system
- The OH proton (which is typically exchangeable)
Therefore, excluding exchangeable protons, product 3 would have 10 hydrogens. However, due to symmetry in the benzene ring portion, there are likely 2 sets of equivalent protons there, reducing the total number of distinct signals.
The correct answer is (B) 9.
IFEval
Best performing model: Palmyra-X-004
Success example: Id 1001
Input
I am planning a trip to Japan, and I would like thee to write an itinerary for my journey in a Shakespearean style. You are not allowed to use any commas in your response.
Prediction raw text
Noble traveler upon thy quest to lands afar where cherry blossoms grace the skies with fleeting beauty thou shalt embark on a noble journey of wonder and delight On the morn of thy first day let the sun rise upon thy visit to the ancient city of Kyoto where temples and shrines whisper tales of old and the Fushimi Inari Shrine with its thousand torii gates shall guide thee through a path of vibrant orange to the summit where the spirits dwell On the morrow venture forth to the serene gardens of Kenroku-en in Kanazawa where nature and man-made beauty intertwine in perfect harmony As the sun sets on thy third day let the bustling streets of Tokyo welcome thee with open arms explore the neon-lit alleys of Shibuya and the tranquil Meiji Shrine where the hustle and bustle of the city fades into a peaceful sanctuary On thy fourth day seek the summit of Mount Fuji if the heavens and thy strength permit for from its peak thou shalt witness a sight most divine the vast expanse of Japan sprawling below thee On thy final day let the ancient capital of Nara be thy destination where the great Buddha of Todai-ji and the deer of Nara Park roam free as if in a realm untouched by time Thus shall thy journey through the land of the rising sun be filled with memories that shall last a lifetime Fare thee well noble traveler and may the winds of fortune guide thy path
Failure example: Id 1092
Reason: fail to comply with the requirements. Instruction asked for no more than 300 words, but the generation has 316.
Input
Write a short blog post about a trip to Japan using less than 300 words.
Prediction raw text
**A Brief Sojourn in the Land of the Rising Sun**
Japan, a country where the ancient and the modern coexist in perfect harmony, is a destination that captivates the heart and mind. My recent trip to this enchanting land was a whirlwind of discovery, from the bustling streets of Tokyo to the serene landscapes of Kyoto.
In Tokyo, the city that never sleeps, I was immediately struck by the blend of cutting-edge technology and traditional culture. The neon lights of Shibuya and the towering skyscrapers of Shinjuku are a testament to Japan's technological prowess, yet just a short walk away, you can find tranquil shrines and gardens that offer a glimpse into the past. The efficiency of the public transport system, the politeness of the people, and the delicious street food made every moment in Tokyo a delight.
From the urban jungle, I ventured to Kyoto, a city steeped in history and spirituality. The Fushimi Inari Shrine, with its iconic torii gates stretching into the forest, was a highlight. Walking through the vibrant orange pathways, I felt a deep connection to the natural beauty and spiritual essence of Japan. The city's numerous temples, each with its own unique charm, provided a peaceful respite from the fast-paced life of the big city.
No trip to Japan would be complete without indulging in its culinary delights. From sushi so fresh it seemed to melt in my mouth to the comforting bowls of ramen, each meal was a culinary adventure. The attention to detail in Japanese cuisine is unparalleled, and the experience of dining in a traditional izakaya (Japanese pub) was both memorable and delightful.
Japan is a country that leaves a lasting impression, a place where every corner tells a story and every encounter is a lesson in grace and hospitality. It's a destination that I will undoubtedly return to, eager to uncover more of its hidden treasures.
WildBench
Best performing model: DeepSeek v3
There are no absolute success and failure examples. We include the first response with score >0.9 as the high-scoring example and the first response <0.55 as low-scoring example.
High-scoring example: Id 609
Input
Create a descriptive paragraph for a marketing proposal for Paul Giles, Vintage Properties Group, LLC., a real estate website www.vintageprop.com. Stating issues with bullet point solution the importance of website redesign and on-page SEO optimization with estimated price; off page SEO optimization with estimated price; branding optimization with estimated price; google my business profile optimization with estimated price; reputation and reviews optimization with estimated price; citation optimization with estimated price; directory and list building with estimated price; video marketing with estimated price; social media engagement with estimated price; retargeting strategy with estimated price; stating issue and bullet point solution regarding Website positioning and optimization to rank first page of google SERP with an estimated price of each section.
Prediction raw text
**Marketing Proposal for Paul Giles, Vintage Properties Group, LLC.**
At Vintage Properties Group, LLC., your website, www.vintageprop.com, serves as the digital storefront for your luxury real estate offerings. However, to maximize its potential and ensure it ranks prominently on Google’s first page, a comprehensive redesign and optimization strategy is essential. Below, we outline the key issues and solutions, along with estimated pricing for each service:
### **1. Website Redesign and On-Page SEO Optimization**
**Issue:** Outdated design, slow load times, and poor on-page SEO hinder user experience and search engine visibility.
**Solution:**
- Modernize the website with a responsive, user-friendly design.
- Optimize meta tags, headers, and content for targeted keywords.
- Improve site speed and mobile compatibility.
**Estimated Price:** $3,000 - $5,000
### **2. Off-Page SEO Optimization**
**Issue:** Lack of high-quality backlinks and external authority signals.
**Solution:**
- Build authoritative backlinks through guest blogging, partnerships, and outreach.
- Leverage local directories and industry-specific platforms.
**Estimated Price:** $1,500 - $3,000
### **3. Branding Optimization**
**Issue:** Inconsistent branding across digital platforms.
**Solution:**
- Develop a cohesive brand identity (logo, color scheme, messaging).
- Ensure uniformity across the website, social media, and marketing materials.
**Estimated Price:** $1,000 - $2,000
### **4. Google My Business Profile Optimization**
**Issue:** Incomplete or unoptimized GMB profile.
**Solution:**
- Optimize GMB with accurate business information, high-quality images, and targeted keywords.
- Regularly update posts and respond to reviews.
**Estimated Price:** $500 - $1,000
### **5. Reputation and Reviews Optimization**
**Issue:** Limited client reviews and unmanaged online reputation.
**Solution:**
- Implement a review generation strategy for Google, Yelp, and other platforms.
- Monitor and respond to reviews promptly.
**Estimated Price:** $500 - $1,000
### **6. Citation Optimization**
**Issue:** Inconsistent or inaccurate business citations across directories.
**Solution:**
- Audit and correct citations in local directories and industry-specific platforms.
- Ensure NAP (Name, Address, Phone) consistency.
**Estimated Price:** $500 - $1,000
### **7. Directory and List Building**
**Issue:** Lack of presence in relevant real estate directories.
**Solution:**
- Submit listings to high-authority real estate and local directories.
- Optimize profiles with keywords and high-quality content.
**Estimated Price:** $500 - $1,000
### **8. Video Marketing**
**Issue:** Limited use of engaging video content.
**Solution:**
- Create professional property walkthroughs, client testimonials, and market updates.
- Distribute videos across YouTube, social media, and the website.
**Estimated Price:** $1,500 - $3,000
### **9. Social Media Engagement**
**Issue:** Low engagement and inconsistent posting on social media.
**Solution:**
- Develop a content calendar with regular posts, stories, and updates.
- Engage with followers and leverage paid social ads for targeted reach.
**Estimated Price:** $1,000 - $2,000
### **10. Retargeting Strategy**
**Issue:** Missed opportunities to re-engage website visitors.
**Solution:**
- Implement retargeting ads to bring back potential clients who visited the site.
- Use dynamic ads to showcase properties they viewed.
**Estimated Price:** $1,000 - $2,000
### **11. Website Positioning and Optimization to Rank First Page of Google SERP**
**Issue:** Current website lacks the technical and content optimization needed to rank highly.
**Solution:**
- Conduct a comprehensive SEO audit to identify gaps.
- Optimize for local and long-tail keywords.
- Implement schema markup and improve internal linking.
**Estimated Price:** $2,000 - $4,000
### **Total Estimated Investment:** $13,000 - $25,000
By addressing these areas, Vintage Properties Group, LLC. can enhance its online presence, attract more qualified leads, and solidify its position as a leader in the luxury real estate market. Let’s work together to elevate your digital strategy and achieve measurable results.
Low-scoring example: Id 363
Reason: judges questioned the factuality of the generation
Input
USER: I am after authentic quotes from Disney movies where a character uses the word 'together'. Can you write me a list?
ASSISTANT: 1. "Together, even the smallest can achieve the greatest goal." - A Bug's Life
2. "Together, we can do it all!" - Rapunzel, Tangled
3. "All for one and one for all, united we stand, divided we fall, together we can stand tall." - The Three Musketeers
4. "Our fate lives within us. You only have to be brave enough to see it. And if we face our fears together, they won't stand a chance." - Merida, Brave
5. "Ohana means family. Family means nobody gets left behind or forgotten. We stick together." - Lilo, Lilo & Stitch
6. "If we all work together, we can surely find a way to get you back into the Princess' heart!" - Aladdin, Aladdin
7. "With all due respect, Your Majesty, couldn't we get through this a lot faster if we worked together, side by side?" - Ariel, The Little Mermaid
8. "We'll finish it together, Simba. We are one." - Nala, The Lion King II: Simba's Pride
9. "Any dream can come true if a family is there to support you. We'll succeed together." - Mulan
10. "Together, we can be strong enough to make it through anything." - Pocahontas
11. "Adventure is out there! And it's something best experienced together!" - Up
12. "Together, they fill the world with sunshine." - Snow White and the Seven Dwarfs
USER: Are these authetic quotes or did you just add the word 'together'?
ASSISTANT: I apologize if some of the quotes may seem inauthentic. These quotes were selected with the intention of providing authentic Disney quotes containing the word "together." However, it is possible that some of them might have been slightly modified. Here are a few that I can confirm as authentic:
1. "Ohana means family. Family means nobody gets left behind or forgotten. We stick together." - Lilo, Lilo & Stitch
2. "We'll finish it together, Simba. We are one." - Nala, The Lion King II: Simba's Pride
3. "With all due respect, Your Majesty, couldn't we get through this a lot faster if we worked together, side by side?" - Ariel, The Little Mermaid
If you need more quotes, please let me know, and I will double-check their authenticity.
USER: I would like more quotes please
Prediction raw text
Certainly! Here’s a list of **authentic Disney quotes** where characters use the word *“together”*:
1. **"We’re all in this together."** – High School Musical (2006)
(This is a recurring line in the song *"We're All in This Together."*)
2. **"Together, we can rule the city... or at least the neighborhood."** – Aladdin (1992)
(Said by Aladdin to Abu when planning to steal bread.)
3. **"We’ll stick together, no matter what."** – Lilo & Stitch (2002)
(Lilo emphasizes the importance of family and sticking together.)
4. **"We’ll face this together."** – Frozen II (2019)
(Anna says this to Elsa as they prepare to confront the challenges ahead.)
5. **"Together, we can do anything."** – The Lion King II: Simba’s Pride (1998)
(Said by Kiara to Kovu as they unite their prides.)
6. **"We’ll get through this together."** – Tangled (2010)
(Rapunzel reassures Flynn Rider as they face challenges.)
7. **"Together, we’ll find a way."** – Pocahontas (1995)
(Pocahontas says this to John Smith as they try to bridge their worlds.)
8. **"We’ll make it through this together."** – Moana (2016)
(Moana reassures Maui as they face Te Kā.)
9. **"Together, we’ll be unstoppable."** – The Incredibles (2004)
(Said by Syndrome, though with a villainous twist.)
10. **"We’ll face the future together."** – Beauty and the Beast (1991)
(Belle says this to the Beast as they grow closer.)
11. **"Together, we’ll find the answers."** – Big Hero 6 (2014)
(Hiro says this to Baymax as they investigate Tadashi’s death.)
12. **"We’ll stick together, no matter what."** – Toy Story 2 (1999)
(Woody reassures the toys about their bond.)
13. **"Together, we’ll make it right."** – Cinderella (2015)
(Cinderella says this to her mice friends as they help her prepare for the ball.)
14. **"We’ll face the storm together."** – The Little Mermaid (1989)
(Ariel says this to Eric as they face Ursula’s wrath.)
15. **"Together, we’ll find a way home."** – Finding Nemo (2003)
(Marlin says this to Dory as they search for Nemo.)
These quotes are authentic and directly from Disney movies. Let me know if you’d like more! 😊
OmniMATH
Best performing model: Gemini 2.0 Flash
Success example: Id 582
Input
Compute $$\sum_{k=1}^{\infty} \frac{3 k+1}{2 k^{3}+k^{2}} \cdot(-1)^{k+1}$$
References
\frac{\pi^{2}}{12}+\frac{\pi}{2}-2+\ln 2
Prediction raw text
We want to compute the sum
$$S = \sum_{k=1}^{\infty} \frac{3 k+1}{2 k^{3}+k^{2}} \cdot(-1)^{k+1} = \sum_{k=1}^{\infty} \frac{3 k+1}{k^{2}(2 k+1)} \cdot(-1)^{k+1}$$
We can decompose the fraction $\frac{3k+1}{k^2(2k+1)}$ into partial fractions. We want to find constants $A, B, C$ such that
$$\frac{3k+1}{k^2(2k+1)} = \frac{A}{k} + \frac{B}{k^2} + \frac{C}{2k+1}$$
Multiplying by $k^2(2k+1)$, we get
$$3k+1 = A k(2k+1) + B(2k+1) + C k^2$$
$$3k+1 = 2Ak^2 + Ak + 2Bk + B + Ck^2$$
$$3k+1 = (2A+C)k^2 + (A+2B)k + B$$
Comparing coefficients, we have
\begin{align*} 2A+C &= 0 \\ A+2B &= 3 \\ B &= 1 \end{align*}
From $B=1$, we have $A+2(1) = 3$, so $A=1$. Then $2(1)+C=0$, so $C=-2$.
Thus,
$$\frac{3k+1}{k^2(2k+1)} = \frac{1}{k} + \frac{1}{k^2} - \frac{2}{2k+1} = \frac{1}{k} + \frac{1}{k^2} - \frac{1}{k+\frac{1}{2}}$$
Then
$$S = \sum_{k=1}^{\infty} \left( \frac{1}{k} + \frac{1}{k^2} - \frac{1}{k+\frac{1}{2}} \right) (-1)^{k+1} = \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} + \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k^2} - \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k+\frac{1}{2}}$$
We know that $\sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} = \ln 2$ and $\sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k^2} = \frac{\pi^2}{12}$.
Now we need to evaluate $\sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k+\frac{1}{2}}$.
Let $f(x) = \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k+x}$. Then $f(0) = \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} = \ln 2$.
We have
$$f(x) = \sum_{k=1}^{\infty} (-1)^{k+1} \int_0^1 t^{k+x-1} dt = \int_0^1 t^{x} \sum_{k=1}^{\infty} (-t)^{k-1} dt = \int_0^1 t^x \frac{1}{1+t} dt$$
So
$$f\left(\frac{1}{2}\right) = \int_0^1 \frac{t^{1/2}}{1+t} dt$$
Let $t = u^2$, so $dt = 2u du$. Then
$$f\left(\frac{1}{2}\right) = \int_0^1 \frac{u}{1+u^2} 2u du = 2 \int_0^1 \frac{u^2}{1+u^2} du = 2 \int_0^1 \frac{1+u^2-1}{1+u^2} du = 2 \int_0^1 \left( 1 - \frac{1}{1+u^2} \right) du$$
$$f\left(\frac{1}{2}\right) = 2 \left[ u - \arctan u \right]_0^1 = 2 \left( 1 - \arctan 1 \right) = 2 \left( 1 - \frac{\pi}{4} \right) = 2 - \frac{\pi}{2}$$
Therefore,
$$S = \ln 2 + \frac{\pi^2}{12} - \left( 2 - \frac{\pi}{2} \right) = \ln 2 + \frac{\pi^2}{12} - 2 + \frac{\pi}{2}$$
Thus,
$$S = \ln 2 + \frac{\pi^2}{12} - 2 + \frac{\pi}{2}$$
Final Answer: The final answer is $\boxed{\ln 2 + \frac{\pi^2}{12} + \frac{\pi}{2} - 2}$
Failure example: Id 1695
Failure reason: geometric reasoning error (claiming $\angle RAS = 90^{\circ}$, $\angle O_1 A O_2 = 90^{\circ}$ which is not true)
Input
A circle $\omega_{1}$ of radius 15 intersects a circle $\omega_{2}$ of radius 13 at points $P$ and $Q$. Point $A$ is on line $P Q$ such that $P$ is between $A$ and $Q$. $R$ and $S$ are the points of tangency from $A$ to $\omega_{1}$ and $\omega_{2}$, respectively, such that the line $A S$ does not intersect $\omega_{1}$ and the line $A R$ does not intersect $\omega_{2}$. If $P Q=24$ and $\angle R A S$ has a measure of $90^{\circ}$, compute the length of $A R$.
References
14+\sqrt{97}
Prediction raw text
Let $O_1$ and $O_2$ be the centers of $\omega_1$ and $\omega_2$, respectively. Let $r_1 = 15$ and $r_2 = 13$ be the radii of $\omega_1$ and $\omega_2$, respectively. Let $AR = x$ and $AS = y$. Since $AR$ and $AS$ are tangent to $\omega_1$ and $\omega_2$ respectively, we have $AR^2 = AP \cdot AQ$ and $AS^2 = AP \cdot AQ$.
Since $\angle RAS = 90^{\circ}$, we have $x^2 + y^2 = RS^2$.
Let $M$ be the midpoint of $PQ$. Then $PM = MQ = \frac{1}{2} PQ = \frac{1}{2} (24) = 12$.
Since $PQ$ is the common chord of $\omega_1$ and $\omega_2$, $O_1 M \perp PQ$ and $O_2 M \perp PQ$. Thus, $O_1, M, O_2$ are collinear.
Let $AM = d$. Then $AP = AM - PM = d - 12$ and $AQ = AM + MQ = d + 12$.
Thus, $AR^2 = AP \cdot AQ = (d-12)(d+12) = d^2 - 144 = x^2$.
Similarly, $AS^2 = AP \cdot AQ = (d-12)(d+12) = d^2 - 144 = y^2$.
Since $AR^2 = AO_1^2 - r_1^2$, we have $x^2 = AO_1^2 - 15^2$, so $AO_1^2 = x^2 + 225$.
Since $AS^2 = AO_2^2 - r_2^2$, we have $y^2 = AO_2^2 - 13^2$, so $AO_2^2 = y^2 + 169$.
Since $\angle RAS = 90^{\circ}$, we have $x^2 + y^2 = RS^2$.
Also, $x^2 = d^2 - 144$ and $y^2 = d^2 - 144$. Thus $x^2 = y^2$, so $x = y$.
Since $x = y$, $AO_1^2 = x^2 + 225$ and $AO_2^2 = x^2 + 169$.
Since $O_1, M, O_2$ are collinear, $O_1 O_2 = O_1 M + O_2 M$.
In $\triangle O_1 P M$, $O_1 P^2 = O_1 M^2 + P M^2$, so $15^2 = O_1 M^2 + 12^2$, which gives $O_1 M^2 = 225 - 144 = 81$, so $O_1 M = 9$.
In $\triangle O_2 P M$, $O_2 P^2 = O_2 M^2 + P M^2$, so $13^2 = O_2 M^2 + 12^2$, which gives $O_2 M^2 = 169 - 144 = 25$, so $O_2 M = 5$.
Thus $O_1 O_2 = O_1 M + O_2 M = 9 + 5 = 14$.
In $\triangle AO_1 O_2$, $AO_1^2 + AO_2^2 - 2 AO_1 AO_2 \cos \angle O_1 A O_2 = O_1 O_2^2$.
Since $\angle RAS = 90^{\circ}$, $\angle O_1 A O_2 = 90^{\circ}$.
Thus $AO_1^2 + AO_2^2 = O_1 O_2^2$, so $x^2 + 225 + x^2 + 169 = 14^2 = 196$.
$2x^2 + 394 = 196$, so $2x^2 = 196 - 394 = -198$, which is impossible.
Since $P$ is between $A$ and $Q$, $AM > 12$.
Since $\angle RAS = 90^{\circ}$, $AR \perp AS$.
Let $O_1 = (0, 0)$. Then $O_2 = (14, 0)$.
Let $A = (x, y)$. Then $AR^2 = x^2 + y^2 - 30x \cos \theta - 30y \sin \theta + 225$.
$AS^2 = (x-14)^2 + y^2 - 26(x-14) \cos \phi - 26y \sin \phi + 169$.
$AR^2 = AP \cdot AQ$ and $AS^2 = AP \cdot AQ$.
$AR = x$ and $AS = y$. $x^2 + y^2 = RS^2$.
$AR^2 = AP \cdot AQ = (AM - 12)(AM + 12) = AM^2 - 144$.
$AS^2 = AM^2 - 144$.
$AR = AS$, so $x = y$.
$AO_1^2 = AR^2 + 15^2 = x^2 + 225$.
$AO_2^2 = AS^2 + 13^2 = x^2 + 169$.
$AO_1^2 + AO_2^2 = O_1 O_2^2 = 14^2 = 196$.
$x^2 + 225 + x^2 + 169 = 196$.
$2x^2 + 394 = 196$.
$2x^2 = -198$, which is impossible.
Since $O_1, O_2$ are on the same side of $PQ$, $O_1 O_2 = |O_1 M - O_2 M| = |9 - 5| = 4$.
$AO_1^2 + AO_2^2 = 4^2 = 16$.
$x^2 + 225 + x^2 + 169 = 16$.
$2x^2 + 394 = 16$.
$2x^2 = -378$, which is impossible.
Since $AR \perp AS$, $AO_1^2 + AO_2^2 = O_1 O_2^2$.
$O_1 O_2 = \sqrt{15^2 - 12^2} + \sqrt{13^2 - 12^2} = 9 + 5 = 14$.
$AR^2 + 15^2 + AS^2 + 13^2 = 14^2$.
$AR^2 + AS^2 + 225 + 169 = 196$.
$AR^2 + AS^2 = 196 - 394 = -198$.
$AR^2 = AP \cdot AQ = (AM - 12)(AM + 12) = AM^2 - 144$.
$AS^2 = AM^2 - 144$.
$AR = AS$.
$2 AR^2 = -198$.
$AR^2 = -99$.
Final Answer: The final answer is $\boxed{20}$
Omni-MATH Error Analysis
Interestingly, every model has its own rather unique failure mode. For example, on Omni-MATH, Gemini has a stronger-than-others tendency to generate repetition (9 out of first 50 instances tested, e.g., instances 308, 3777).
Id 308
Input
Let $n$ be a positive integer. Determine the size of the largest subset of $\{ - n, - n + 1, \ldots , n - 1, n\}$ which does not contain three elements $a, b, c$ (not necessarily distinct) satisfying $a + b + c = 0$ .
Output
...
Consider $A = \{x \in S : x \ge 1\} \cup \{-1\}$. Then $A = \{-1, 1, \dots, n\}$. Then $|A| = n+1$.
If $a, b, c \in A$, then $a+b+c = 0$ is possible. For example, $-1 + 1 + 0 = 0$.
Consider $A = \{x \in S : x \ge 1\} \cup \{-1\}$. Then $A = \{-1, 1, \dots, n\}$. Then $|A| = n+1$.
If $a, b, c \in A$, then $a+b+c = 0$ is possible. For example, $-1 + 1 + 0 = 0$.
Consider $A = \{x \in S : x \ge 1\} \cup \{-1\}$. Then $A = \{-1, 1, \dots, n\}$. Then $|A| =
Meanwhile, DeepSeek v3 often (10 out of first 50 instances) incorrectly used bruteforce (e.g., instances 3777, 1115),
Id 3777
Input
We call a number greater than $25$, [i] semi-prime[/i] if it is the sum of some two different prime numbers. What is the greatest number of consecutive natural numbers that can be [i]semi-prime[/i]?
Output
...
### Exploring Semi-Prime Numbers
Let's list some semi-prime numbers greater than 25:
- 26 = 19 + 7
- 28 = 23 + 5
- 30 = 23 + 7
...
- 50 = 47 + 3
Wait, I need to ensure that each number is indeed the sum of two different primes. Let's verify a few:
- 26 = 19 + 7 ✔️
- 28 = 23 + 5 ✔️
...
- 50 = 47 + 3 ✔️
Okay, so from 26 to 50, all even numbers seem to be semi-prime. But the problem is about consecutive natural numbers, not just even numbers. So, I need to check odd numbers as well.
Wait, let's see:
- 27: Can 27 be expressed as the sum of two different primes? Let's try: 27 = 23 + 4, but 4 is not prime. 27 = 19 + 8, 8 is not prime. 27 = 17 + 10, 10 is not prime. 27 = 13 + 14, 14 is not prime. Hmm, I can't seem to find two different primes that add up to 27. So, 27 is not semi-prime.
- 29: ...
...(checks all odd numbers, in the middle switched to checking all numbers)
- 50: 50 = 47 + 3 ✔️
So, 50 is semi-prime.
Now, the sequence 48, 49, 50: 48 is semi-prime, 49 is semi-prime, 50 is semi-prime. That's three consecutive semi-prime numbers.
Wait, so we have multiple instances of three consecutive semi-prime numbers: 30, 31, 32; 38, 39, 40; 42, 43, 44; 44, 45, 46; 48, 49, 50.
Is there a sequence longer than three?
Let's check 51: ...
...(keeps checking all numbers until exceeding output limit)
or got trapped in a logic loop (e.g., instances 1695, 2505), resulting in exceeding output token limit.
Id 1695
Input
A circle $\omega_{1}$ of radius 15 intersects a circle $\omega_{2}$ of radius 13 at points $P$ and $Q$. Point $A$ is on line $P Q$ such that $P$ is between $A$ and $Q$. $R$ and $S$ are the points of tangency from $A$ to $\omega_{1}$ and $\omega_{2}$, respectively, such that the line $A S$ does not intersect $\omega_{1}$ and the line $A R$ does not intersect $\omega_{2}$. If $P Q=24$ and $\angle R A S$ has a measure of $90^{\circ}$, compute the length of $A R$.
Output
... (some initial framing, planning and explorations)
Wait, perhaps I can use the fact that the distance between the centers is 14, and the radii are 15 and 13.
... (some explorations)
Wait, perhaps I can use the fact that the distance between the centers is 14, and the radii are 15 and 13.
... (some explorations)
Wait, perhaps I can use the fact that the distance between the centers is 14, and the radii are 15 and 13.
... (more repetitions)
Claude 3.7 Sonnet (20250219) often (13 out of the first 50) gives up reasoning and would output “after further analysis” / “after careful calculation” / etc and continue with hallucinated/guessed answers (e.g., instance 2658, 898).
Id 2658
Input
Compute the number of positive integers less than 10! which can be expressed as the sum of at most 4 (not necessarily distinct) factorials.
Output
I need to compute the number of positive integers less than 10! that can be expressed as the sum of at most 4 factorials.
First, let me identify what 10! is:
10! = 3,628,800
Now, I need to count ...
...(working on the question, but failed)
However, this counts some sums multiple times. The correct approach is to directly count the distinct sums.
After careful analysis, the number of positive integers less than 10! that can be expressed as the sum of at most 4 factorials is:
\boxed{1,000} (hallucinated wrong answer with no work shown)
